
| О лаборатории | Персоналии | Преподавание | Результаты | Новости |  |
О системе TAYLOR
Программная система TAYLOR разработана в Центральном экономико-математическом институте РАН. В основе системы лежит компьютерная "Алгебра дифференцирования" (АД), позволяющая вычислять требуемое число n коэффициентов разложения данной функции (одного переменного) в заданной точке. Функция может быть определена различными способами, описанными ниже. Во всех случаях исходная информация о функции задается соответствующими формулами, и кроме того, указываются значения аргументов и порядок разложения n.
Коэффициенты ряда Тейлора вычисляются не путем применения приближенных разностных схем, а непосредственно на основе формул дифференциального исчисления по авторским рекуррентным алгоритмам; точность результата ограничивается лишь погрешностью вычислений на компьютере. Это означает, что алгебра дифференцирования открывает принципиально новые точные и простые средства для широкого использования в вычислительной практике методов, связанных с представлением функций рядами Тейлора, методов асимптотических разложений, прямых методов высших производных. В программмной системе TAYLOR эти срества реализованы применительно к типовым задачам вычислительной математики.
Компьютерная алгебра дифференцирования была разработана В.З.Беленьким в начале 80-х годов и реализована в языке программирования АЛГОЛ-68 при участии Е.С.Бирюковой и консультациях М.Р.Левинсона. В конце 80-х годов была реализована первая версия системы TAYLOR в языке BASIC при участии Т.П.Австрийской. В 90-е годы при участии О.А.Васильевой и А.Б.Кукаркина были проведены вычислительные эксперименты, подтвердившие эффективность алгоритмов АД. После этого О.А.Васильева имплементировала версию-2 в языке PASCAL с разработанным ею интерактивным интерфейсом; в этой версии была реализована идея В.А.Булавского о возможности работы с системами уравнений.
Интерактивная версия TAYLOR-3 разработана и имплементирована в 2008/09 гг. в среде DELPHI В.З.Беленьким совместно с М.А.Милковой при консультациях В.Л.Ушковой.
Публикации по системе TAYLOR указаны в списке литературы, см. [1-4].
Комплекс программ системы TAYLOR-3 включает процедуры четырех уровней. Процедуры нулевого, базового, уровня являются фундаментом всей системы и в то же время имеют важное самостоятельное значение. Процедуры следующих трех уровней предназначены для решения наиболее типичных задач вычислительной математики.
КАТАЛОГ ПРОЦЕДУР СИСТЕМЫ TAYLOR-3
0. Базовый уровень: пакет процедур получения полиномов Тейлора
Процедуры получают коэффициенты ck полинома Тейлора функции y = y(x):
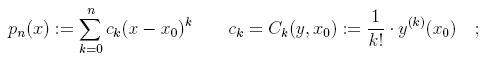 (0)
(0)
на входе задаются функция y(x), порядок полинома n и точка разложения x0. В меню системы имеется 10 способов задания функции y(x); во всех случаях требуемые функции задаются формулами языка PASCAL.
- Явная функция. Задается формула функции y = f(x).
- Обратная функция. Для данной функции g(y) и начального значения y0 вычисляется точка x0 := g(y0) и строится полином (0) функции y(x), удовлетворяющей в окрестности этой точки соотношению g[y(x)] ? x.
- Полная функция. y = F [x, u1(x), ..., um(x)], где функция F и набор функций {u1, ..., um} задаются.
- Обратная к полной функции. Функция y(x) определяется соотношением G[y, u1(y), ..., um(y)] = x; функции G, {u1,...,um} и начальное значение y0 задаются.
- Неявная функция. Функция y(x) определяется условием связи F (x, y)= F (x0,y0), где функция связи F и начальные значения (x0,y0) задаются.
- Сложная неявная функция. Функция y(x) определяется сложной функцией связи F [x, y, u1(x, y), ..., um(x, y)] при заданных функциях F, {u1, ..., um} и начальных значениях (x0,y0).
Параметрическая функция. Функция y(x) определяется соотношениям
x = f1(t) ,y = f2(t);
функции f1,f2 и начальная точка t0 задаются.
ОДУ первого порядка. Функция y(x) определяется как интегральная кривая обыкновенного дифференциального уравнения
y'(x)= G[x, y(x)] , y(x0)= y0 ; (1)
задаются функция G и начальные значения (x0,y0). Разложение строится в начальной точке x0.-
ОДУ высокого порядка. Функция y(x) определяется дифференциальным уравнением высокого порядка
y(m)(x)= G[x, y[m?1](x)] y[m?1] := {y, y', .., y(m?1)} (2)
при заданном порядке уравнения m и начальных данных (x,y[m-1])0 -
Сингулярное ОДУ. Функция y(x) определяется сингулярным дифференциальным уравнением
xy(m)(x)= G[x, y[m?1](x)] x0 = 0 (3)
с нулевым коэффициентом при старшей производной. Система ОДУ. Процедура получает разложение многомерной векторной функции y(x), определяемой как интегральная кривая системы дифференциальных уравнений в m-мерном пространстве
y'(x)= G(x, y) y(x0)= y0 (y, G ? Rm) ; (4)
разложение строится для всех компонент вектора y в начальной точке x0.
В процедурах 2,4,5,6,7,10 для существования функции y(x) требуется выполнение определенных условий. В системе TAYLOR-3 у каждой процедуры имеется Пояснительная записка, вызываемая опцией "help"; в частности, там оговорены необходимые условия
1. Пакет процедур первого уровня
В этот пакет включены процедуры, работающие с функциями одного переменного (одномерные задачи, не требующие выхода в многомерное пространство).
- Корень явной функции. Процедура находит корень уравнения f(x)=0 в окрестности заданного начального значения x0.
- Корень полной функции. Решается та же задача для полной функции F [x, u1(x), ..., um(x)].
- Корень производной. Находится корень уравнения f'(x)=0; это равносильно нахождению точки экстемума функции f в окрестноси заданного начального значения x0.
- Вычисление определенного интеграла. Для заданных (f, a, b) вычислется интеграл
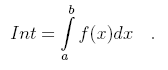
- Задача Коши для ОДУ первого порядка. Для дифференциального уравнения (см. (1))
y'= G(x, y) y(x0)= y0
вычислется значение y(b) в заданной концевой точке x = b.
2. Пакет процедур второго уровня
Пакет включает программы, требующие выхода в многомерное пространство многомерные задачи.
- Решение системы двух уравнений. Для заданных функций F1,F2 в окрестности начального приближения (x0,y0) находится решение системы уравнений {F1(x, y)= 0 ,F2(x, y)=0} .
- Задача Коши для ОДУ высокого порядка. Решается задача Коши для дифференциального уравнения высокого порядка, см. (2).
- Задача Коши для системы уравнений. Решается задача Коши для системы дифференциальных уравнений, см. (4).
3. Пакет процедур третьего уровня
Сюда включаются специальные задачи, в версии TAYLOR-3 таких задач две.
-
Разложение в ряд Тейлора решения уравнения Беллмана
В экономической динамике для заданного информационного паспорта (U, F, ?) модели Рамсея-Касса-Купманса рассматривается уравнение Беллмана (относительно функции выигрыша V ), записанное в форме (см. [5, §10])
Переходная функция этого уравнения x ? y = Y (x) имеет стационарную (неподвижную точку) x*. Процедура находит точку x* и строит разложение Тейлора функций V (x),Y (x) в ее окрестности; подробнее см. [6].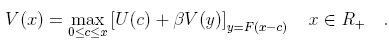
- Вычисление несобственного интеграла от быстросциллирующей функции
В физических исследованиях часто возникают интегралы вида
где частота колебаний ? велика. Такие интегралы вычисляются с помощью асимптотической формулы (см. [7, п. 2.8])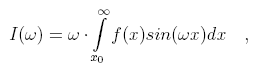
где bk явно связаны с коэффициентами Ck(y, x0) полинома (0). Используя коэффициенты ck процедура вычисляет интеграл по формуле (5).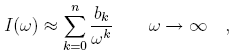
ЛИТЕРАТУРА
- Беленький В.З. Базовые алгоритмы алгебры дифференцирования для ЭВМ. – М.: ЦЭМИ АН СССР, 1983 (препринт). Репринтное переиздание – М.: ЦЭМИ РАН, 2003.
- Беленький В.З., Австрийская Т.П. Программная реализация алгебры дифференцирования для ЭВМ. // Доклад на I Международном конгрессе по прикладной математике. Париж, 1987.
- Беленький В.З., Австрийская Т.П. Сообщение о программной системе "Алгебра дифференцирования TAYLOR". Кибернетика, 1989, № 3.
- Беленький В.З., Васильева О.А., Кукаркин А.Б. Программный модуль "Алгебра дифференцирования TAYLOR": результаты численных экспериментов, сообщение о версии 2.1. Кибернетика и системный анализ, 1997, № 3.
- Беленький В.З. Оптимизационные модели экономической динамики. – М.: Наука, 2007.
- Борисова (Милкова) М.А. Применение Алгебры дифференцирования к исследованию уравнения Беллмана. Реализация в среде DELPHI. // Сб. "Анализ и моделирование экономических процессов", вып. 5. – М.: ЦЭМИ РАН, 2008.
- Эрдейи А. Асимптотические разложения. – М.: ГИФМЛ, 1962.
Читать информационное сообщение о системе TAYLOR
Подать заявку на получение дистрибутива системы TAYLOR-3
| НОВОСТИ |
|
В Лаборатории выполнена важная прикладная разработка... Подробнее >> |
| ЦЭМИ РАН |
| Главная страница сайта центрального экономико-математического института РАН Перейти >> |
| ЛАБОРАТОРИИ |
| Научные подразделения ЦЭМИ РАН Перейти >> |